![]() 分数の計算について
分数の計算について![]()
![]() 分数の計算について
分数の計算について![]()
【分数の2通りの使い方】
分数には大きく分けて2通りの使い方がありますが、これを混同してしまうことが分数の計算をするときに間違う最大の原因となります。
「2リットルの水が入ったPETボトルから、花瓶に水をとる」ということについて考えてみます。
【割合分数(分割分数)】
① 「PETボトルから花瓶に水を![]() とる」というのは、実際には1リットルをとることになります。
とる」というのは、実際には1リットルをとることになります。
①のような分数表現を割合分数または分割分数といいます。この場合は全体の量が決まって始めて目的の量が決まるものですから、相対的な量の表現方法であるといえます。
【量分数】
② 「PETボトルから花瓶に水を![]() リットルとる」というのは、まさしく字の通りで、
リットルとる」というのは、まさしく字の通りで、![]() リットル、すなわち0.5リットルをとることになります。
リットル、すなわち0.5リットルをとることになります。
②のような分数表現を量分数といいます。この場合は全体がどうであるかはまったく関係がなく、目的の量は不変的なものですから、絶対的な量の表現方法であるといえます。
【英語圏と日本語の分数表現の文化の違いについて】
日本では![]() 千円とか
千円とか![]() 時間(8時半などとはいいますし、昔は
時間(8時半などとはいいますし、昔は![]() 時間を小半といっていましたが)とかいう表現はあまり使わないので、量分数を使う慣習がないのに対して、英語では
時間を小半といっていましたが)とかいう表現はあまり使わないので、量分数を使う慣習がないのに対して、英語では![]() ドル(half
dollar)、
ドル(half
dollar)、![]() 時間(half
hour)、
時間(half
hour)、![]() 時間(quarter
hour)や25セントをクウォーター(quarter)というなどの分数表現が日常的に存在します。
時間(quarter
hour)や25セントをクウォーター(quarter)というなどの分数表現が日常的に存在します。
たぶん、小学校で分数を学習するときに、分数には2通りの表現方法があるというのをあまり強調することはないと思いますが、それは日本の文化とも深い関わりがあると考えます。量分数の表現をあまりしない環境で育った子供たちに、2つの表現の違いを説明すると余計にややこしくなるという訳です。
【”分数+分数”について】
【例題1】![]() +
+![]() についてAさんは次のように考えました。
についてAさんは次のように考えました。
まず、![]() を2個のりんごのうちの1個分、
を2個のりんごのうちの1個分、![]() を3個のりんごうちの1個分と考えると、それらを合わせて、結果は5個のりんごのうちの2個分になるので
を3個のりんごうちの1個分と考えると、それらを合わせて、結果は5個のりんごのうちの2個分になるので![]() だから
だから![]() +
+![]() =
=![]() となります。アレッ?
となります。アレッ?
それでは、2と3の最小公倍数である6を全体の個数として考え直してみましょう。
![]()
全体の量(個数)を統一するというのが”通分”であり、分数と分数を足したり引いたりするときは、必ずこの操作が必要です。
それでは、次に全体の量が決まっている量分数の足し算について考えてみましょう。
【量分数の足し算】
【例題2】![]() cm2と
cm2と![]() cm2を足すと何cm2になるでしょうか。
cm2を足すと何cm2になるでしょうか。
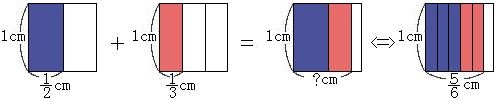
下の図のように、1辺が1cmの正方形を全体であると仮定します。
さて、![]() は青の面積で、
は青の面積で、![]() は赤の面積で表されますが、それらを足した結果を出すためには互いの分数の橋渡しをする”共通となるものさし”が必要になってきます。ここで、
は赤の面積で表されますが、それらを足した結果を出すためには互いの分数の橋渡しをする”共通となるものさし”が必要になってきます。ここで、![]() を”共通のものさし”にすると、
を”共通のものさし”にすると、![]() は
は![]() が3個分で、
が3個分で、![]() は
は![]() が2個分なので足すことができて、
が2個分なので足すことができて、![]() +
+![]() =
=![]() と計算することができます。したがって、答えは
と計算することができます。したがって、答えは![]() cm2となります。
cm2となります。
ここで、”共通のものさし”である![]() は
は![]() と
と![]() の分母である2と3の最小公倍数から求めることができます。
の分母である2と3の最小公倍数から求めることができます。
【”分数×分数”について】
【分数の足し算と掛け算】
小学校の教科書では、まず「分数の足し算と引き算」を学習し、そのあと「分数の掛け算、割り算」の順に学習していきます。まず、分数の足し算や引き算では分母どうし、分子どうしを通分してから計算することを学習するのですが、分数の掛け算は分母どうし、分子どうしをそのまま掛け合わせるだけでよいので、掛け算のところでその意味をきっちり説明してあげないと、前述のAさんのように足し算と掛け算の計算を混同してしまうことがあります。
【分数の掛け算】
【例題3】1m2の広さの壁を塗るのに2![]() dl(デシリットル)のペンキが必要でした。3
dl(デシリットル)のペンキが必要でした。3![]() m2の広さの壁を塗るには何dlのペンキが必要でしょうか?
m2の広さの壁を塗るには何dlのペンキが必要でしょうか?
2![]() ×3
×3![]() を計算すればよいのはすぐに分かると思いますが、その結果はどうなるのでしょう。
を計算すればよいのはすぐに分かると思いますが、その結果はどうなるのでしょう。
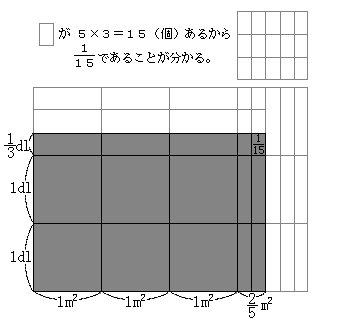 右の図のように、長方形の横を”壁の面積”、また縦を”壁1m2当りに必要なペンキの量”とすると、壁全体を塗るのに必要なペンキの量はグレーの部分の面積ということになります。
右の図のように、長方形の横を”壁の面積”、また縦を”壁1m2当りに必要なペンキの量”とすると、壁全体を塗るのに必要なペンキの量はグレーの部分の面積ということになります。
【”分数÷分数”について】
いよいよ分数の割り算です。「どうして分数の割り算は割る方の分数の分母と分子をひっくり返して掛けるのか?」ということについては、これまで多くの方法が研究され、教科書でも数十年前よりはずっと分かり安い解説をしています。ですから、教師のほうで教材をいかに工夫し、興味を持たせて子供たちに教授するかが最大のテーマであるといえるでしょう。ここでは、「単位すりかえ法」と「分数直線法」の2つの方法を使ってご説明いたします。
【単位すりかえ法】
畳を一畳というような感覚で3![]() m2(=
m2(=![]() m2)の広さの壁を一壁ということにすると、1m2の広さの壁は
m2)の広さの壁を一壁ということにすると、1m2の広さの壁は![]() 壁ということになります。すると【例題4】は「一壁を塗るのに2
壁ということになります。すると【例題4】は「一壁を塗るのに2![]() dl(デシリットル)のペンキが必要でした。
dl(デシリットル)のペンキが必要でした。![]() 壁を塗るには何dlのペンキが必要でしょうか?」という表現にすることができます。
壁を塗るには何dlのペンキが必要でしょうか?」という表現にすることができます。
すなわち2![]() ×
×![]() を計算する問題にすりかえることができた訳です。あとは分数の掛け算を理解していれば簡単な問題になります。
を計算する問題にすりかえることができた訳です。あとは分数の掛け算を理解していれば簡単な問題になります。
【分数直線法】
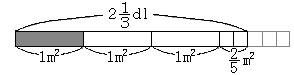
壁の広さとペンキの量の関係を上図のような分数直線で表してみます。すると、1m2当りに必要なペンキの量は図のグレーの部分の面積を求めればよいことが分かります。
3![]() m2=
m2=![]() m2だから、2
m2だから、2![]() dlには
dlには![]() m2が17個分対応しています。そこで、まず2
m2が17個分対応しています。そこで、まず2![]() ÷17として
÷17として![]() m2に対応するペンキの量が何dlかを考えます。次に1m2は
m2に対応するペンキの量が何dlかを考えます。次に1m2は![]() が5個あるから、それを5倍すればよい訳です。すなわち、
が5個あるから、それを5倍すればよい訳です。すなわち、
2![]() ÷3
÷3![]() =2
=2![]() ÷
÷![]() =(2
=(2![]() ÷17)×5=2
÷17)×5=2![]() ×
×![]() と考えることができます。
と考えることができます。
【最後に】
前述しましたように、英語圏に比べて日本での分数表現の文化はそれほどではありません。また、分数表現よりも百分率(パーセント)の方が分かりやすい事があります。
例えば確率の問題でお馴染みの「サイコロを振ったときに1の目が出る確率は![]() である。」というのがありますが、これを「サイコロを振ったときに1の目が出る確率は約16.7パーセントである。」と表現したほうがや分かりやすいと感じる方は多いと思います。
である。」というのがありますが、これを「サイコロを振ったときに1の目が出る確率は約16.7パーセントである。」と表現したほうがや分かりやすいと感じる方は多いと思います。
実は「分数の計算」については、”その意味付けが難しい”というので昭和26年の学習指導要領で、小学校のカリキュラムから「分数」がなくなったことがあったのです。しかし、その後の学力調査で小学生の学力低下が問題となり昭和33年に再び現在のように「分数」が小学校の5年生と6年生に戻ってきました。小学生の算数嫌いはこの頃から始まっているといわれていますから、「分数の計算」を理解することの難しさを感じるとともに、「分数の計算」を教授する側のより一層の創意と工夫が望まれます。