よいテストと偏差値の関係

【なぜ偏差値か？】

　｢偏差値｣は分かり難いものでありながら、受験を控えた子供たちと保護者にとっては、進学先を決定する最も重要な”ものさし”として存在しています。一方では人を数量でランクづけする偏差値は、人間らしさを失わせる悪の根元であるとして、公立中学校でも業者の模擬テストを使って進路指導することを止めたのはまだ最近のことです。

　いまや子供の数が激減し、あと数年後には大学全入時代が来るといわれています。中学校入試も年々その激しさを増し、有名進学塾に通う子供は小学校の先生のことより塾の先生のことをより信頼するようになってしまいました。コンピュータ機能の飛躍的な進展によって大量の数値演算処理が可能になった結果、受験産業は全国的な模擬試験を実施し、テスト結果の評価に偏差値を利用しました。その模試は大規模であるがゆえに信頼性の高いものとなり、偏差値によって細かく輪切りにされた中学、高校、大学の合否予想にまで欠かすことのできない判断材料になったのです。それによって、さらに偏差値による大学、高校の輪切り現象がすすむことになりました。

さて、ここではその逆の発想といってはなんですが、「偏差値の何たるかも理解せずに、進学先を偏差値に合わせる」ことが恐ろしい結果を生み出すこともあるということをポイントにしてご説明していきたいと思います。
　

【偏差値について】

　テストで１００点をとったとしても、平均点が高いときと低いときでは、その重みも変わってくることはなんとなく理解できますが、「標準偏差」が大きいときと小さいときでも偏差値が大きく異なることを理解されている方は少ないかも知れません。

【標準偏差（Standard Deviation）と偏差値（Deviation Value or T−score）】

あるテストを受験した集団の１つ１つの数値が違っていることを｢数値が散らばっている｣とか、｢数値がばらついている｣といいます。個人の得点の散らばり度合いを数値で表すとき、散布度というものを考えます。これにはいくらかの種類がありますが、代表的なものに標準偏差があります。
偏差値は、標準偏差を利用して算出されます。式だけをみても分かり難いので、下の３つの表を使ってご説明します。

さて、A〜Hさんの８人が、１０点満点のテストを受験したとします。このとき、下の例１〜例３の表ような場合について一緒に考えてみたいと思います。

�@ まず、各データと平均点（すべて６点にしてあります。）との差を計算します。この数値を偏差といいます。
偏差＝（得点−平均点）

�A 偏差を２乗（平方ともいう）して合計します。この数値を偏差平方和または変動といいます。
変動＝（Aさんの偏差）²+・・・+(Hさんの偏差）²

�B 変動を受験人数（８人）で割ります。これを分散といいます。
分散＝変動÷８

�C 分散の平方根（の正の方）をとります。これを標準偏差といいます。
標準偏差＝分散の平方根　　

上の３色の棒グラフをご覧下さい。この棒グラフをヒストグラムといいます。緑のヒストグラムでは、その得点分布は１点から１０点までバラバラに散らばっています。また、青のヒストグラムでは、ほとんど平均点の６点に集中しています。それに比べて、赤のヒストグラムは６点を中心にして、比較的なだらかな山になっています。どの場合も平均点は６点ですが、例１の場合は６点の人は自分より上に４人いるので順位は５位、例２の場合は１人いて順位は２位、例３の場合は２人いて順位は３位となります。同じ平均点をとっているにもかかわらず、分布の違いによって順位は違ってくるのです。

｢平均値は、集団の真ん中の値である｣というのは分布の仕方によっては正しいとはいえないのです。

【分布の色々】

　これまでに統計学者や数学者によって色々な分布が理論的に研究されてきました。量的（連続）データの分布は正規（ガウス）分布、対数正規分布、指数分布などが、質的（離散）データの分布は二項分布、ポアソン分布などがあります。統計学上基本となる分布は正規分布と二項分布ですが、正規分布は偏差値と深い関わりがあります。

二項分布は高校の数学で確率を勉強するときに必ず出てくるもので、サイコロ投げの実験などの理論分布です。
ポアソン分布は”まれ”にしか起こらない現象の起こる回数の分布で、ある都市で１日に交通事故で死亡する人の数の分布や鉄板の一定面積中にあるキズの数の分布などがあります。
正規分布は、自然現象や社会現象の中に広く見られる分布で、ある畑にある芋の大きさの分布や工場で内容物の量が一定になるようにセットしているが、機械や環境の変化などが要因で起こるその重さの誤差の分布などがあります。

正規分布の発見者の一人はガウス（Carl Friedrich Gauss 1777〜1855）ですが、アメリカの数学者アドレイン（1775〜1843）もほとんど同時期に独立にこの分布に到達しました。ガウスは天文学や測地学の観測データの処理をもとに観測誤差論の確立を目指してこの分布を発見しました。

【正規分布（ガウス分布）】

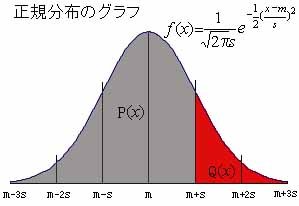
偏差値はそもそも平均値を偏差値50に，その標準偏差を10になるように換算し、個人の成績を相対的にみるために考えられた数値で、受験者全体の得点が正規分布をしているとみなし、各人の得点が平均から標準偏差の何倍離れたところにいるかを表す数値です。 成績のヒストグラムが正規分布に近い場合は、受験者人数、平均（ｍ）、標準偏差（ｓ）の３点セットがわかれば正規分布表の値から大体の順位がわかるのです。 例えば受験者が５００人いて、平均点が６０点、標準偏差が１２であったとき、７２点を取った人の順位は７２＝６０＋１．０ｓだから自分より上に１５．８７％の成績上位者がいて、自分は５００×０．１５８７�垂V９だから、８０番目位にいるということになります。 ここで、内申書に存在する５段階あるいは１０段階評価について考えてみましょう。これも何を隠そう正規分布に従って１〜５あるいは１〜１０を割り振っているのです。成績の優秀な子供の多い学校とそうでない学校の格差が出るとか、５に近い４の生徒と３に近い４の生徒が同じというのはちょっと納得がいきませんよね。まあ、これも運といってしまえばそれまでですが...

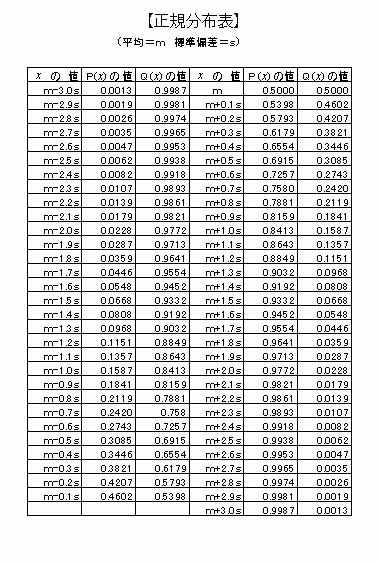前述のように、偏差値を計算するときには、｢人の能力や学力は正規分布する｣ということを大前提にして話をすすめている訳です。ですから、｢良いテスト｣とは、平均点当りに多くの生徒が集まり、平均点から離れるにつれてだんだんと少なくなるようなものということになるのです。しかし、試験作成者がそのつもりで作っても実際にはそんなにうまくはいきません。
また、事前に範囲の限られた試験であったり、何度も同じ事を繰り返して覚えさせるための試験などのように、試験の種類によっては到底”正規分布にはならない”であろうと予想されるものもあります。それでは、歪んだ分布になったとき、偏差値を過信するとどんなことになるかをご説明します。

【あるテストでの考察】

�@ ある先生が抜打ちテストを実施したとします。突然にテストがあったので、日ごろからしっかり勉強していた人と、そうでない人がいたので、例１のヒストグラムようなバラバラに散らばった得点分布になってしまいました。

�A 先生は近いうちにまた抜打ちテストをすると予告しましたが、”近いうちに”という言葉を軽く考えていた人とそうでない人がいたので、例３のヒストグラムのようななだらかな山のような得点分布になりました。

�B 最後に先生は明日テストをすると予告したので、みんなが同じように勉強した結果、例２のヒストグラムのような６点のところに集中する得点分布になりました。

【歪んだ分布で偏差値を過信すると恐ろしい結果になる】

さて、ここで�@→�A→�Bの順での「Bさんの得点と偏差値」に注目して下さい。

�@ ３点で、偏差値は４１です。

平均点が６点なので、日ごろからあまり勉強していたとはいえませんでしたが、Bさんは自分より得点の低い人がいることを知り、（←上より下をみる子供が多いんですよね！？）また、”近いうちに”といわれたのであまり勉強しませんでした。

�A ４点で、偏差値は３６です。

Bさんは自分が一番点数の悪かったことに気付きました。偏差値も３６です。あれっ？１点多くとったのに偏差値は５も下がっている！！Bさんは明日試験があると聞き、いままでの自分の考え方を反省し、しっかり勉強しました。

�B ５点で、偏差値は３０です。

他のみんなもしっかり勉強していたので殆ど差がつきませんでした。しっかり勉強し、得点も回を重ねる毎に上昇したBさんでしたが、なんと偏差値は最悪の３０になってしまいました。

さて、以上のような話で、偏差値を理解していないと恐ろしいことが起こることに驚かれたことと思います。

前述しましたように、例１や例２などのような分布や、その他にも山が２つとか３つできたりするような分布は正規分布と比べて”ひずんだ分布”と考えることができます。このような分布の場合は、偏差値を使ってものごとを考えてはいけないということを知っておく必要があります。

【偏差値と進路決定】

　前述しましたように、ある集団にテストをした場合、平均と標準偏差が計算できます。また、これによって偏差値も計算できます。

自分の志望校の過去の入試問題の傾向、問題の難易度、採点基準を十分に研究した模擬試験を数回受験し、しかも受験者集団がほとんどかわらないような場合に偏差値を比べるというのならばそれなりの意味があるでしょう。

しかし、いままで中学校で採用されていたような業者の模試というのは、大規模ではあっても、ある特定の学校を対象にしたものでもないし、受験者集団が同じであるという保証はまったくありません。また難易度や採点基準も一定である保証はないのです。

ですから、子供達には偏差値や大学合格数などに惑わされず、自分の実力を自分で決めずに、できれば将来何をしたいのかということも含めてしっかり勉強し、志望校の校風などもよく理解して進路を決定するようにして欲しいとおもいます。

【最後に】

　人間というのはけっして単純に成績や五段階評価などの数字でランクづけできるものではなく、数字で表されない素晴らしい点を誰しも必ず持っているものです。やはり日頃から子供に一番近くにいる保護者や教師が子供の良い点に気付き、子供が落ち込んで自信をなくしているときに励ましてやれるような存在になりたいものです。人を叱ることはとても簡単なことですが、人を褒めるにはその人のことをいつも見ていなければなりません。子供たちによりよい環境を残していってやることが、子供たちの先輩としての私達おとなの役割ではないでしょうか...