さて、音楽もＬＰレコードやカセットといったアナログからＣＤやＭＤといったデジタルの時代になりました。２０００年の冬から本格的にテレビもデジタル放送時代に突入し、音声や画像がすべて０と１で表現されるようになりました。さて、今回は【第弐話】芸術・自然と数学の融合でも触れた数列について、音という私達の感覚の世界に登場するもののお話です。

【音階の数学的な考察について】

現在学校の音楽の授業で習う音階は、普通ドレミファソラシドですよね。必然的にその音を演奏する楽器も、それに基づいて作られています。これは日本の音階（レミソラシド）とは異なり、西洋からきた音階です。でも、ドレミファソラシドってどうして決まったのでしょうか？これには数学的な説明が必要になってきます。それは、人が聞いて心地よい和音（調和）は、簡単な整数比で表せるからです。
この第什壱話だけはちょっと｢おもしろ数学講座｣とはいかず、数学的に易しく説明することができませんでした。中世ヨーロッパでは音楽は数学的４学科のなかの１つとされ、学問領域における音楽学・音律論として位置付けられていたからです。音楽理論の知識がある方や音楽に興味のある方は是非ご一読下さい。

西洋音階を最初に考えたのは古代ギリシャの｢三平方（ピタゴラス）の定理｣でも有名なピタゴラスであるといわれています。その音階を自然（ピタゴラス全）音階といいますが、その他に西洋音階の代表的なものとして、平均律音階、純正調音階があります。これらはいずれもドレミファソラシドを確定させていますが、正確には少しずつ音が異なります。それでは、その音階の決定法について数学的にみていきましょう。

【自然音階】

【弦の長さと音の関係について】

音階において、最初に登場したのは、西暦紀元前45年にピタゴラスによって発見された自然（ピタゴラス全）音階です。ピタゴラスは、弦の長さと音階の関係を以下の�@〜�Bの規則によって完成させました。

ピタゴラス音階の構成理論では

主音に対する周波数比ｈで、任意の整数ｘ、-1≦y＜10の範囲の整数yによってｈ＝２^ｘ３^ｙで表せる音階

また、１オクターブ内に限定して考える場合は、周波数が２倍になったとき、ちょうど１オクターブ上の音が得られるので、1≦ｈ<2とすればよい。

ということになっていますが、具体的には次のように考えていきます。

�@長さ１の音をドとすると、長さ（２^-1３⁰）の音は１オクターブ高い音（ド）である。
�A長さ１の音をドとすると、長さ（２¹３^-1）の音は５度高い音（ソ）である。
�B�@、�Aとは逆に、１オクターブ低いドは弦の長さを２倍に、５度低い音は倍にすればよい。

さて、この規則を用いて弦の長さを変えて、ドやソ以外の音もつくってみましょう。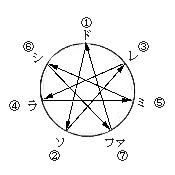

音	音を作る方法	弦の長さ	周波数比：ｈ
レ	ソの音を５度上げてから１オクターブ下げる	××２＝	２3３-2
ラ	レの音を５度上げる	×＝	２4３3
ミ	ラの音を５度上げてから１オクターブ下げる	××２＝	２6３4
シ	ミの音を５度上げる	×＝	２8３5
ファ	１オクターブ高いドの音を５度下げる	×＝	２-2３1

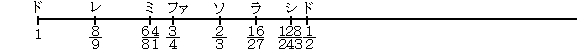
数列とは｢ある一定の規則にしたがって並んだ数の列｣のことで、２，５，８，１１，１４，・・・のようにはじめの数に同じ数を次々と加えていってできる数列を等差数列（Arithmetical Progression）であるということは【第弐話】芸術・自然と数学の融合フィボナッチ数列と黄金比でも触れました。
さらに、１，，，，，・・・で並んでいる数列は、この逆数をとると、はじめの数にを次々と加えていった数列になります。

このような、各項の逆数が等差数列になる数列を調和数列（Harmonic Progression）といいます。自然音階では最初の規則で登場した３項１，，がこの順に調和数列になっていますよね。
英語で和音のことをハーモニー（Harmony）といいますから、洒落た命名だと思うのですがいかがでしょうか。

この考え方は中国でも三分損益という音律測定法で説明されていました。その後、中国から日本に伝わったのは、江戸時代の頃で、学者が度量衡と同列に扱っていたそうです。

さて、自然音階では、転調する際に複雑になるという欠点や、１オクターブを１２分割すると、正確にはｙ＝−１のときとｙ＝１１のときで同じｈ＝１にはなりません。具体的にいうと、最後のファをつくるのはシからではなく、１オクターブ高いドを５度下げてつくっています。のシから始めると、１オクターブ高いドは262144/531441≒0.4932701となり、にはなりません。１６９２年に中根璋が『律原発揮』でもこの問題を指摘しました。そこで平均律音階が登場することになりました。

【平均律音階】

この音階は、近代ヨーロッパ音楽では、転調が自由であり、ピアノや五線譜にも適しているためによく用いられてきました。

平均律音階の構成理論は

主音に対する周波数比の列{ｈ_j}が等比数列をなし、ｈ₀＝1のとき、ある正の整数ｋに対してｈ_k＝2となるとき、{ｈ_j}をｋ分割平均律全音階である。

周波数比が等比数列になっているということは、隣り合う２音の音程がすべて同じであるという意味です。

また、ｈ₀＝１，ｈ_k＝２は１オクターブがｋ個の音で構成されているという意味です。

実際に計算すると ｈ_j＝２^j/k　　

ということになっていますが、これについても同様に、具体的に考えていきましょう。

例えばピアノの鍵盤には白鍵と黒鍵がありますが、１オクターブの間はこれらによって１２に分けられています。

音の振動数は１オクターブでちょうど２倍になるので、２を１２に分割します。

振動数で考えると、分割比Ｘは、Ｘ¹²＝２だから、両辺の常用対数をとって、

１２log10Ｘ＝log10２　　　ここでlog10２≒0.3010だから、log10Ｘ＝log10２＝×0.3010≒0.0251

よって　Ｘ≒1.06 となります。
つまり、ある音の半音高い音は、その音の振動数を１．０６倍した振動数をもつ音で、全音高い音は１．０６²倍の周波数比をもつ音ということになります。こうして得られた音階を平均律音階といいます。

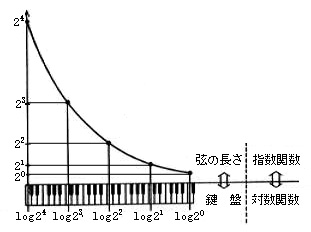
平均律音階は、ピタゴラス音階のように直接的な音の調和を問題にせずに、数学的な合理性を優先して決定されています。よって、移調が容易になり、どの音を主音に選んでも音の高低が変わるだけで、曲の流れには変化が起こりません、ただし、音の調和という点では少し問題が残りますが、実際に演奏してみるとその差は一般人にはほとんど聞き分けることができないそうです。

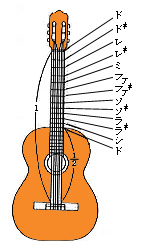
左の図はチェンバロという楽器にみたてています。音域がピアノよりも狭く、４から５オクターブの楽器です。例えば、図のように４オクターブとして１オクターブごとのドの音に注目すると、弦の長さは次々に２を掛けたものになっています。そして、それぞれの弦の長さの底を１０とする対数（常用対数）をとってみるとチェンバロそのものの楽器の形になっているのです。

ピアノの場合は８オクターブにもなるので、チェンバロのようにすると、一番高いドの音の弦を１０ｃｍとして理論上最も長い弦が１２．８ｍにもなってしまうので、弦の太さを変えたり、銅巻き線を用いることによって調整をしています。

さらに、人類は完全な調和を求め、それは純正調という音階の各音の音程関係を簡単な整数比で表す方法に委ねられることになりました。

　【純正調全音階】

純正調全音階の構成理論では

主音に対する周波数比ｈで、任意の整数ｘ、-2≦y≦2の範囲の整数y、-1≦z≦1の範囲の整数zによって
ｈ＝２^ｘ３^ｙ５^zで表せる音階

ということになっています。具体的には次のように考えていきます。

�@弦楽器である音を奏でると、整数倍の周波数をもった倍音が生じる。

�A�@の現象から、周波数比が簡単な整数比となる２つの音は調和する。

上述のピタゴラス音階の構成理論【弦の長さと音の関係について】での説明のように、1≦ｈ<2とし、底を２とする対数をとると、

0≦x+ylog₂３+zlog₂５＜1

で、この条件に-2≦y≦2の範囲の整数y、-1≦z≦1の範囲の整数zの、条件を加えて（ｘ,ｙ,ｚ）の組を求めると、ｈが小さいものから並べると、下表のようになります。

音階	ド			レ	ミ		ファ			ソ	ラ			シ		ド
	１															２
周波数比 x,y,z	0,0,0	4,-1,-1	1,-2,1	-3,2,0	1,1,-1	-2,0,1	2,-1,0	-5,2,1	6,-2,-1	-1,1,0	3,0,-1	0,-1,1	4,-2,0	0,2,-1	-3,1,1

音純正調全音階の１６個の音から７個のドレミファソラシの音を選んだのは次の規定に沿っています。

【純正調音階について】

�@最も簡単な整数比として　Ｇ（ソ）＝，Ｆ（ファ）＝　を考える。

�AＣ（ド）＝１としたとき、Ｇ/Ｃ＝２Ｃ/Ｆが成り立ち、低いドとソの音程が、ファと高いドの音程に等しいことがわかる。この音程は完全５度と呼ばれ、最もよく調和するとされている。

�BＣ＜Ｄ＜Ｅ＜Ｆ　　，　　Ｇ＜Ａ＜Ｂ＜Ｃ　　，　　Ｃ：Ｅ：Ｇ＝Ｆ：Ａ：２Ｃ＝Ｇ：Ｂ：２Ｄと規定する。

�Bの規定によって、主要３和音を構成することができます。また、各和音の３つの音の周波数比がすべて同一になるようにしています。

�@〜�Bから、　Ｄ（レ）＝９/８

Ｅ（ミ）は２つの可能性があり、６/５のときＡ（ラ）＝，Ｂ（シ）＝　（純正調短音階）

　　　　　　　　　　　　　　　５/４のときＡ（ラ）＝，Ｂ（シ）＝　（純正調長音階）

となります。

【最後に】

　人間の音楽的感性は、音の物理的な調和の上に根拠を置いて育ってきました。その意味では、音階は必然的にドレミファソラシドになっているということになります。しかし、人間の耳が１オクターブ中で１２個程度の音に違いしか聞き比べることができないのでしょうか？実際は、もう少し多くの音を聞き比べられるそうで、１８分割平均律音階や２４分割平均律音階の研究をしている方もいらっしゃいます。この新しい音感の世界によって作曲された音楽を是非とも聞いてみたいものです。